Assuming a thin beam, simply supported at the ends, with a beam length of 27mm, thickness of 0.25mm, and midpoint deflection of 0.86mm, the maximum tensile strain Emax can be estimated from
Emax=t/2R
where t is the thickness and R is the radius of curvature. Given the radius of curvature, 106mm, which can be estimated from the deflection and length, the estimated maximum tensile strain in the material is 1.2*10-3. The limited applicability of isotropic beam theory dictates the need for more complex composite beam theory, such as the 2D laminate approach with asymmetric layup; however, the estimate is reasonable by being less than the measured strain to failure of typical bulk 3D carbon-carbon composites in tensile testing.
Additional evidence for residual stress is demonstrated by the bimetallic strip behavior of the sample during heating and cooling, depicted in Fig.3 for the curved sample at different temperatures on the surface of a hot plate. On heating, the curvature decreases slightly. This is to be expected, because the thermal expansion of the fibers in the longitudinal direction is lower than that of the matrix and fibers in the transverse direction. The difference will cause the matrix and transversely oriented fibers, which are in tension, to expand more than the x-direction fibers, which are in compression. The reverse occurs on cooling the sample in liquid nitrogen, which causes a small increase in sample curvature. That the curvature returned to its initial condition at room temperature shows that the changes are reversible within the temperature range, and that, therefore, bonding integrity between the composites of the composite remains good.
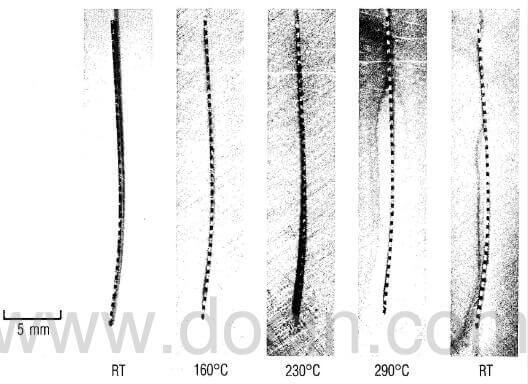
fig.3-changes-in-curvature-versus-temperature-of-0.25-mm-slice-of-2-2-3-composite
The change in curvature with temperature oan also be related to the degree of undercooling below the stress-free temperature, at which the beam is not curved. Using a linear thermal expansion model, a study of residual stress in a thin beam of copper bonded to a ceramic showed that 1/R, where R is the radius of curvature, is proportional to the degree of under-cooling below the stress-free temperature, Ts, or
1/R=k(T5-T)
where k is a constant and T is temperature. For a small degree of curvature, the midpoint displacement, d, is proportional to 1/R. Thus, at a given temperature, T, d is proportional to (Ts-T), or
d=k'(Ts-T)
where k’ is a constant. From the observed values of d and T at two temperatures, which implies that the fiber and matrix material bond
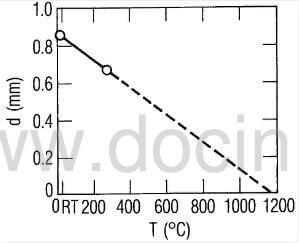
fig.4-measured-maximum-diaplacement-versus-temperature
well over a fairly wide temperature range and that the matrix remains sufficiently intact to retain some residual stress. The presence of residual stress and the implied large undercooling contrast with other indications that stress tends to be removed by matrix microcracking because of the large undercooling below the expected stress-free temperature, which is above 2000°C, where stress relaxation by creep becomes significant in carbon-carbon composites.
In conclusion, thin slices of 3D cartesian weave carbon-carbon composites with asymmetric cross section have been demonstrated to contain residual stresses as a reult of thermal expansion anisotropy. The slices are curved, with longitudinal reinforceing filaments in residual compression and transverse fibers and matrix material in residual tension.